Numerical solution of nonlinear PDEs

• Finite volume schemes for convection-dominated drift-diffusion problems
• Complete flux and Scharfetter-Gummel schemes for nonlinear diffusion
• Physics preserving methods

Charge transport in semiconductors

• PDE models coupled to continuum mechanics (finite strain), atomistic fluctuations, optics (Helmholtz)
• Drift diffusion simulation tools ChargeTransport.jl and ddfermi
• Applications such as bent nanowires, perovskites, memristors and quantum wells

Meshfree methods

• RBF collocation and interpolation
• Convergence and stability for multilevel methods
• Anisotropic (surface) mesh improvement

Perovskites

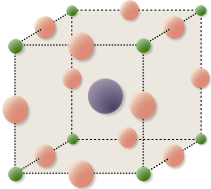
About ten years ago engineers showed for the first time that low-cost perovskites could be used to convert sunlight into electricity. Since then their efficiency has greatly improved, giving hope to replace or modify (via tandem solar cells) less efficient yet widely-used silicon-based solar cells soon. Ion movement affects the cells and is challenging to simulate due to stiffness.

Cooperations: RG1, RG3, Helmholtz Zentrum Berlin, University of Oxford, Inria Lille/University of Lille

Nanowires

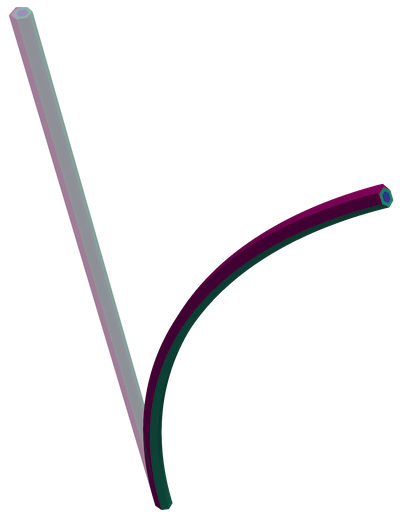
Nanowires have many potential applications, for example they may be used to build even smaller MOS transistors. Useful electronic properties of these thin wires can be controlled via elastic strain. However, unexpectedly slow charge carrier transport require careful simulations combining charge transport with continuum mechanics to explain the cause.

Cooperations: RG1, RG3, Paul-Drude-Institut (PDI), Leibniz Institute for High Performance Microelectronics (IHP)

Memristors

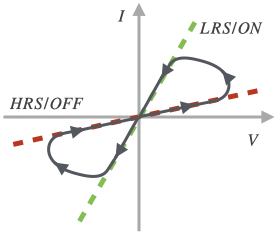
The von Neumann architecture is far from ideal for AI applications due to its unacceptably high energy consumption. Memristors help to emulate the energy efficiency of human brains. The group develops complex charge transport models which incorporate mobile point defects and Schottky barrier lowering to theoretically understand the shape and asymmetries of the hysteresis curves observed in experiments.

Cooperations: TU Ilmenau

Quantum wells

The goal of this project is to model and simulate random alloy fluctuations in band edge profiles within a full device. To achieve this, we combine random atomic fluctuations in band edges with macroscale drift diffusion processes. The spatially randomly varying band edges are implemented in ddfermi. Quantum effects are taken into account via localization landscape theory (LLT).

Cooperations: RG1, Tyndall National Institute (Cork, Ireland)

Imaging techniques

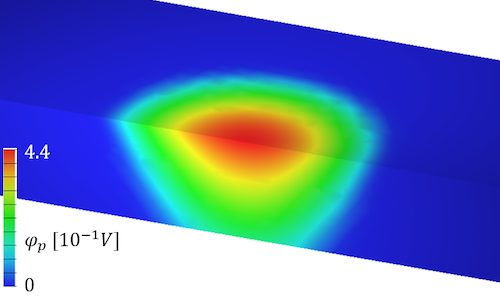
Several semiconductor-based imaging techniques help to predict fluctuations in doping profiles such as the laser beam induced current (LBIC) or the lateral photovoltage scanning (LPS) method. Mathematically, this translates into an inverse problem which is solved via machine learning techniques.

Cooperations: RG3, Institut für Kristallzüchtung, University of Florence, SISSA (Trieste, Italy)

Lasers

Semiconductor-based LiDAR (light detection and ranging) sensors improve autonomous driving as they are accurate, comparatively small and thus mass market friendly. Moreover, high precision lasers are needed in quantum metrology and quantum computing. The group extends the van Roosbroeck model to incorporate additional physical effects (heterostructures, heat transport and light emission) by coupling a charge transport model to a Helmholtz problem.

Cooperations: RG1, RG2, RG3, Ferdinand-Braun-Institut (FBH)

Neural networks/surrogate models

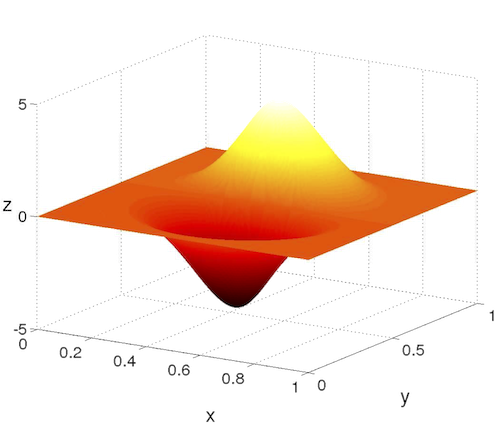
The core of machine learning algorithms consists of a (usually high-dimensional) optimization problem. To find a minimizer within such complex structures it is often beneficial to resort to surrogate models, which are minimized instead of the original problem. Due to the curse of dimensionality it is often not feasible to build meshes. For this reason meshfree methods help to efficiently build surrogate models.

Cooperations: WG DOC, University of Florence, SISSA